

a) Rigid Motion 1 Description: Reflection through line (hint sketch in BD above) Label the following square if the following rigid motion was performed on the square shown above it. jnt1 rigidBodyJoint ( jnt1, revolute ) body1.Joint jnt1 Add the rigid body to the tree. Label the image of each rigid motion in the provided blanks. Replace the joint by assigning a new rigidBodyJoint object to the body1.Joint property. By default, the rigidBody object comes with a fixed joint.
The MOST IMPORTANT rule to remember for the regents is when they ask you if any of these transformations are congruent, write "A reflection/translation/rotation is a basic rigid motion, therefore distance is preserved." Click Here for the practice questions on rigid motions. body1 rigidBody ( b1 ) Create a revolute joint. To graph a reflection across the line y=-x, the formula is (x,y)→(-y,-x) We call a figure that is about to undergo a transformation the. To graph a reflection across the line y=x, the formula is (x,y)→(y,x) Why is a dilation not a rigid motion Use the facts above to clearly explain your answer. To graph a reflection over the y-axis, use the formula (x,y)→(-x,y) To graph a reflection over the x-axis, use the formula (x,y)→(x,-y) Rigid motions are a translation or a rotation for. The central line is called the mirror line. Step-by-step explanation: A rigid transformation of a graph leaves the size and shape of a graph unchanged. What are the characteristics of rigid transformations A rigid transformation does not change the size or shape of an object. A dilation is a transformation that changes the size of a figure. The only transformation that is not a rigid motion is dilation. Every point is the same size as the orginal image, and every point is the same distance form the central line. Rigid motions are transformations that move an image, but do not change the size. ReflectionĪ reflection is a flip over a line. the a represents the change in the x axis and the b represents the change in the y axis. 4.1.1 Orthogonal Transformations There are two ways of thinking about an orthogonal transformation Aand its action on an orthonormal basis, (Eq. so such a transformation will either preserve or reverse the orientation. To graph a translation use the formula (x,y)→(x+a,y+b). play such an important role in the study of rigid body motion, we need to explore the properties of orthogonal transformations in some detail. Orientation-Reversing Transformations A rigid motion maps directed lines to.

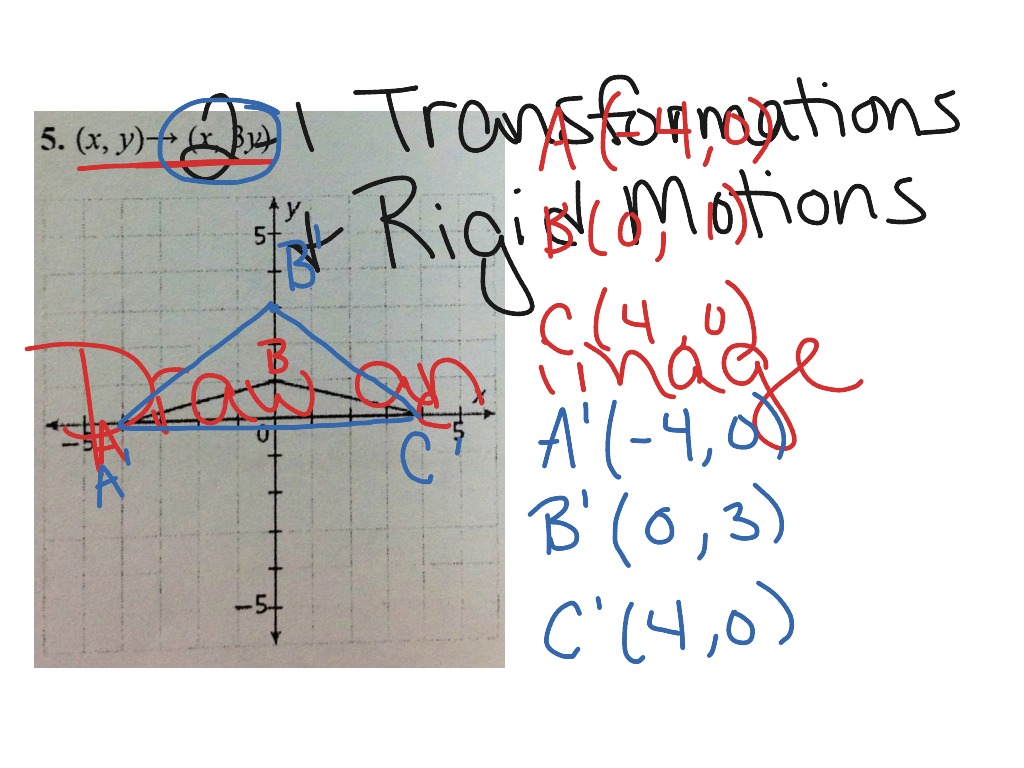
To graph a rotation 180 degrees in either direction around the origin, use the formula (x,y)→(-x,-y)Ī translation simply means moving without rotating, resizing or anything else, just moving. To graph the rotation 90 degrees counterclockwise about the origin, use the formula (x,y)→(-y,x) To graph the rotation 90 degrees clockwise about the origin, use the formula (x,y)→(y,-x) In other words, one point on the plane, the center of rotation, is fixed and everything else on the plane rotates about that point by a given angle.Ī way to make rotations easier to graph is by using coordinate notation. Notes for Rigid Motions Notes for Rigid Motions Types of Rigid Motions RotationĪ transformation in which a plane figure turns around a fixed center point.


 0 kommentar(er)
0 kommentar(er)
